What happens when two waves meet?

That, basically, is what this topic is about. The word "superposition' refers to the way that the waves can add or cancel each other then they meet.

This topic is about what happens when two waves meet each other. In the previous topic on waves, I have described some of the basic features like displacement, amplitude, wavelength, frequency and velocity. I have also mentioned standing wave, which happens two waves with similar amplitudes travelling in opposite directions meet.

Just to recap - a standing wave happens when two identical waves travelling in opposite directions meet. The result is a wave that has fixed zero amplitude at equally spaced intervals - as if the wave is not travelling. Hence the name "standing wave".

The standing wave is a simple example of superposition.

In this article, we shall what happens when when two waves spreading out in 2 dimensions meet - like on a water surface. And then we shall see how this can help us understand - or "discover" - that light is actually a wave.

Water wave is probably the most familiar type of of wave we can see. You see it when you drop your coin in a bucket of water, and when you drop a stone into a pool. In each case, you would probably see circular rings appearing and moving out from the coin or stone hits the water.

The circular rings or ripples are waves. Maybe very small waves, but still waves. These waves are created at at the point when the stone hits the water surface. This creates an up down motion that travels outwards.

Lets wait a bit for the water surface to settle back to rest. Then drop two small stones into the the water, a few centimetres apart. You will see ripples forming again. Each stone forms its own set of ripples. Then the two sets of ripples meet, you will find a more complex pattern that looks quite different from the original circular ripples.

It looks like the two sets of ripples force their ways into each other and mess up the nice circular rings. This action and effects of two waves meeting each other is called interference.

The simplest type of interference is a simple game that children sometimes play. Find a rope, tie one end to a pole, pull the other end loosely, and start shaking up and down.

You will see a wave appearing near your hand. This wave travels to the pole and reflects back in your direction. Since you are still shaking your end, the new waves you are making overlaps with these reflected waves.

Being part of the action, it would be a bit difficult for you to see this clearly. But if you ask a friend to take a video of the string, you can see that you have generated a wave on the string.

And there is something strange about this wave. Although most parts of the string are moving up and down, the wave shape is not travelling at all!

There are regular points along the string that remain at rest, while the rest of the string in between points are shaking up and down vigorously. This makes it look like the wave shape is not actually travelling, but kind of just standing or resting on the string.

So this is called a "standing wave". Another name is "stationary wave", but I prefer "standing wave" as it sounds simpler.

When the reflected wave overlaps with the outgoing wave to form a new shape on the string, the effect is called "interference".

But how exactly do they interfere? Answer: the separate displacements the two waves simply add together to give the result shape. This way of getting the final waveform is called "superposition" - the title of this topic.

This example is about wave on a string. But as is often the case with physics, ideas like this can often be extended in other ways - like from string wave to water wave, sound wave, light wave, ... and from just 1 dimension along a string to 2 dimensions on a water surface or 3 dimensions in air.

After understanding the action in waves interfering with each other along the 1 dimension of a string, we come to the main theme of this topic - waves interfering in 2 (and maybe 3) dimensions.

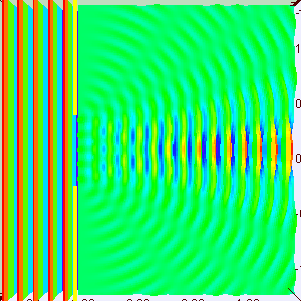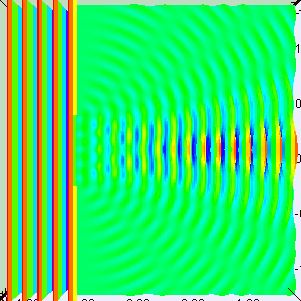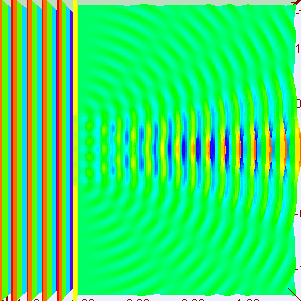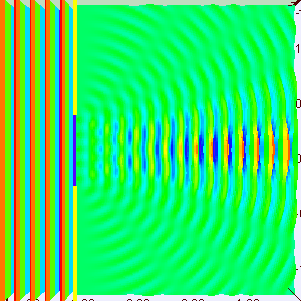
This time, we go from the string to the water surface. For a quick preview of what I am going talk about, have a look at the animated images above. The images show what look like waves travellimg along a water surface from left to right.

The figure on the left shows the wave hitting a wall with a small hole. Most of the wave is blocked, but a small bit leaks through the hole. Notice that the small bit of wave that leaks through slowly gets wider and wider as it travels to the right.

This spreading or bending around edges is called diffraction, and is what waves normally do.

If we make the same hole wider, the wave would spread less. So there is more diffraction for narrower gap, and less diffraction for wider gap.

I have just given the standard textbook explanation on why waves coming through the gap spreads sideways.

But we should actually turn the question round and ask - why shouldn't it spread sideways? After all, if you disturb the water by throwing in a stone, the resulting wave spreads everywhere.

So to summarise: wave through narrow gap spreads more, wave through wide gap spreads less.

Note: "Narrow gap" means maybe just a few wavelengths wide. "Wide gap" means many wavelengths wide.

Now we come to the main part of this topic, which often comes out in exam questions - two-source interference.

The image above on the right shows what it looks like looks like the diffraction example that I described above. But there are 2 holes instead of 1 hole. So a small bit of wave from the left goes through both holes, and spread out on the right sit.

The spreading from each hole happens in the same way as the diffraction described above for the single hole. What's new here is: what happens when the spreading waves from the 2 holes overlap?

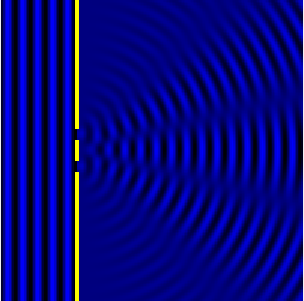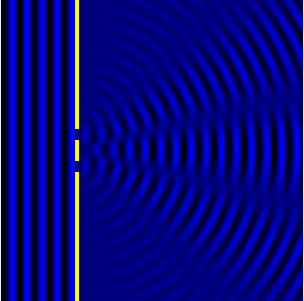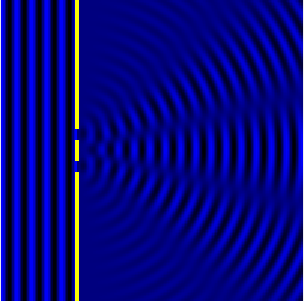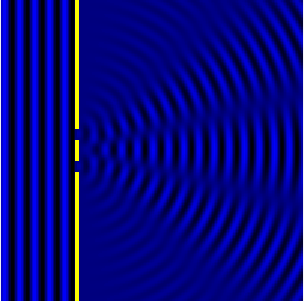
What happens in this image is that the overlapping waves split into 5 broad "beams". You can see them if you look at the image for a few seconds.

In between beams, the wave amplitude is small or zero. They don't describe it this way in schools or textbooks, but I like to think of this "two-source interference" as a 2D standing wave.

If you are learning this for the first time, you may find it a bit curious but nothing special. Just another water wave.

But this effect has actually allowed scientists to discover that light is actually a wave, a discovery in hstory that has led further discoveries in physics and modern inventions like laser technologies.

It was about 200 years ago.

As an example, suppose that I want to show that light is actually a wave. How on earth do I do that? Maybe after watching how waves spread out from a river into the sea, I get an idea. Why not just make two small holes side by side like the water experiment above. Then see if light coming through would split into a few beams like the water wave.

Even for the water wave, this is not easy. I have to adust the width and distance of the holes until they are close enough to the wavelength before I can see the interference pattern clearly. And I have no idea what the wavelength of light might be. This is going to be really tedious.

But we can get some idea from the water wave - of the hole size is close to the wavelength, the wave would diffract more - or spread sideways more. Since we can see that sunlight does not spread around big holes, we clearrly have to go small. So I would start making the holes smaller and smaller until the sunlight coming through seem to spread out a bit and case a light spot a bit bigger than the hole itself.

Then I make another hole next to it so that the second light spot overlaps with the first one.

This is my guess of how Thomas Young did his experiment. With no A level physics tutor to guide him, he had to be super patient and super motivated. And he probably failed many times (I guess). But finally one day in 1807, he saw this:

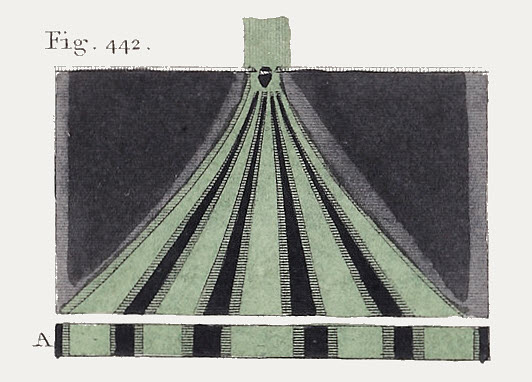
The sunlight coming through the two slits split into a number of beams!

Light is a wave !!

And so we have to learn this today in physics.

There are a few simple equations students have to learn for this topic. I shall just mention that these equations allow us to calculate the wavelength of the light from the fringe spacing and some measurements of the holes setup.

Using simple maths and geometry, Young obtained a formula that can be used to calculate wavelength of light from the spacing of the fringes:

wavelength = distance between slits x spacing between fringes / distance to screen

Using the distances he measured from his sunlight setup, Young was probably able to calculate that the wavelength of sunlight ranges from 400 nanometers (violet light) to 800 nanometers (red light).

By adding more slits at equal spacing, the fringes are still the same spacing apart but each fringe gets narrower and narrower. This means that fringe spacing can be measured more and more accurately, so wavelength measurement also becomes more and more accurate.

Such a setup with many equally spaced slits for light to come through is called a diffraction grating.

This measuring technique was later made very accurate by adding many more slit at the same spacing. When light through all the slits interfere at the screen, the fringes produced are still at the same spacing, but become very sharp, thin lines.

This makes it possible to measure the spacing very accurately, so the wavelength calculated from this is also very accurate.

And so it was 100% confirmed that light is a wave and not particles. For about 100 years after that, everyone one was happy. And then scientists discovered that light can somehow knock out electrons from some types of metals - a process called photoelectric effect. It was difficult to explain, until Albert Einstein suggested that light is made up of particles that can knock out the electrons.

And so we know today that light is both a wave and a particle, depending now how we choose to observe it - which can actually sound crazy.

You can learn these concepts and more at Dr Hock's physics tuition.